| ルンゲクッタ法で様々な連立微分方程式を解く数値計算例(Java) |
- プログラムソース (ラングフォードの方程式)
import java.io.*;
/*ラングフォードの方程式
dx/dt=(z-0.7)x-3.5y
dy/dt=3.5x+(z-0.7)y
dz/dt=a+z-z^3/3-(x^2+y^2)(1+0.25z)
をルンゲクッタ法で解く
*/
class Runge
{
public static void main()
{
double t,x,y,z,dt,tmax;
double k0[]=new double[3],k1[]=new double[3],k2[]=new double[3],k3[]=new double[3];
Runge f=new Runge();
dt=0.01;
tmax=100.0;
x=y=z=1.0; //初期値
try
{
FileWriter fw=new FileWriter("output.data");
for(t=0.0;t<tmax;t+=dt)
{
k0[0]=dt*f.f1(t,x,y,z);
k0[1]=dt*f.f2(t,x,y,z);
k0[2]=dt*f.f3(t,x,y,z);
k1[0]=dt*f.f1(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k1[1]=dt*f.f2(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k1[2]=dt*f.f3(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k2[0]=dt*f.f1(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k2[1]=dt*f.f2(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k2[2]=dt*f.f3(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k3[0]=dt*f.f1(t+dt,x+k2[0],y+k2[1],z+k2[2]);
k3[1]=dt*f.f2(t+dt,x+k2[0],y+k2[1],z+k2[2]);
k3[2]=dt*f.f3(t+dt,x+k2[0],y+k2[1],z+k2[2]);
x=x+(k0[0]+2.0*k1[0]+2.0*k2[0]+k3[0])/6.0;
y=y+(k0[1]+2.0*k1[1]+2.0*k2[1]+k3[1])/6.0;
z=z+(k0[2]+2.0*k1[2]+2.0*k2[2]+k3[2])/6.0;
fw.write(x + " " + y + " " + z + "\n");
}
fw.close();
}
catch(Exception e)
{
System.out.println(e);
}
}
double f1(double t,double x,double y,double z)
{
double r;
r=(z-0.7)*x-3.5*y;
return r;
}
double f2(double t,double x,double y,double z)
{
double r;
r=3.5*x+(z-0.7)*y;
return r;
}
double f3(double t,double x,double y,double z)
{
double r,a;
a=0.6; //この数値を変えることによって多様な解が得られる
r=a+z-z*z*z/3.0-(x*x+y*y)*(1.0+0.25*z);
return r;
}
}
- GNUPLOT出力結果

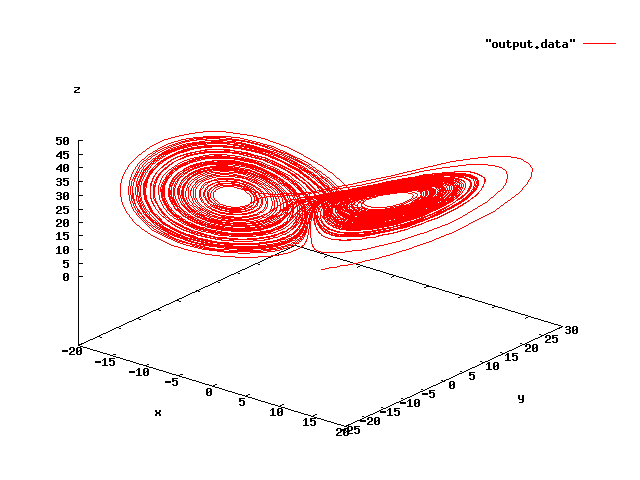
- プログラムソース (ローレンツの方程式)
import java.io.*;
/*ローレンツの方程式
dx/dt=10(y-x)
dy/dt=28x-y-xz
dz/dt=-(8/3)z+xy
をルンゲクッタ法で解く
*/
class Runge
{
public static void main()
{
double t,x,y,z,dt,tmax;
double k0[]=new double[3],k1[]=new double[3],k2[]=new double[3],k3[]=new double[3];
Runge f=new Runge();
dt=0.01;
tmax=100.0;
x=y=z=1.0; //初期値
try
{
FileWriter fw=new FileWriter("output.data");
for(t=0.0;t<tmax;t+=dt)
{
k0[0]=dt*f.f1(t,x,y,z);
k0[1]=dt*f.f2(t,x,y,z);
k0[2]=dt*f.f3(t,x,y,z);
k1[0]=dt*f.f1(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k1[1]=dt*f.f2(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k1[2]=dt*f.f3(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k2[0]=dt*f.f1(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k2[1]=dt*f.f2(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k2[2]=dt*f.f3(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k3[0]=dt*f.f1(t+dt,x+k2[0],y+k2[1],z+k2[2]);
k3[1]=dt*f.f2(t+dt,x+k2[0],y+k2[1],z+k2[2]);
k3[2]=dt*f.f3(t+dt,x+k2[0],y+k2[1],z+k2[2]);
x=x+(k0[0]+2.0*k1[0]+2.0*k2[0]+k3[0])/6.0;
y=y+(k0[1]+2.0*k1[1]+2.0*k2[1]+k3[1])/6.0;
z=z+(k0[2]+2.0*k1[2]+2.0*k2[2]+k3[2])/6.0;
fw.write(x + " " + y + " " + z + "\n");
}
fw.close();
}
catch(Exception e)
{
System.out.println(e);
}
}
double f1(double t,double x,double y,double z)
{
double r;
r=10*(y-x);
return r;
}
double f2(double t,double x,double y,double z)
{
double r;
r=28*x-y-x*z;
return r;
}
double f3(double t,double x,double y,double z)
{
double r;
r=-8/3*z+x*y;
return r;
}
}
- GNUPLOT出力結果
- プログラムソース (レスラーの方程式)
import java.io.*;
/*レスラーの方程式
dx/dt=-y-z
dy/dt=x+0.34y
dz/dt=0.4x-4.5z+xz
をルンゲクッタ法で解く
*/
class Runge
{
public static void main()
{
double t,x,y,z,dt,tmax;
double k0[]=new double[3],k1[]=new double[3],k2[]=new double[3],k3[]=new double[3];
Runge f=new Runge();
dt=0.01;
tmax=300.0;
x=y=z=1.0; //初期値
try
{
FileWriter fw=new FileWriter("output.data");
for(t=0.0;t<tmax;t+=dt)
{
k0[0]=dt*f.f1(t,x,y,z);
k0[1]=dt*f.f2(t,x,y,z);
k0[2]=dt*f.f3(t,x,y,z);
k1[0]=dt*f.f1(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k1[1]=dt*f.f2(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k1[2]=dt*f.f3(t+dt/2.0,x+k0[0]/2.0,y+k0[1]/2.0,z+k0[2]/2.0);
k2[0]=dt*f.f1(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k2[1]=dt*f.f2(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k2[2]=dt*f.f3(t+dt/2.0,x+k1[0]/2.0,y+k1[1]/2.0,z+k1[2]/2.0);
k3[0]=dt*f.f1(t+dt,x+k2[0],y+k2[1],z+k2[2]);
k3[1]=dt*f.f2(t+dt,x+k2[0],y+k2[1],z+k2[2]);
k3[2]=dt*f.f3(t+dt,x+k2[0],y+k2[1],z+k2[2]);
x=x+(k0[0]+2.0*k1[0]+2.0*k2[0]+k3[0])/6.0;
y=y+(k0[1]+2.0*k1[1]+2.0*k2[1]+k3[1])/6.0;
z=z+(k0[2]+2.0*k1[2]+2.0*k2[2]+k3[2])/6.0;
fw.write(x + " " + y + " " + z + "\n");
}
fw.close();
}
catch(Exception e)
{
System.out.println(e);
}
}
double f1(double t,double x,double y,double z)
{
double r;
r=-y-z;
return r;
}
double f2(double t,double x,double y,double z)
{
double r;
r=x+0.34*y;
return r;
}
double f3(double t,double x,double y,double z)
{
double r;
r=0.4*x-4.5*z+x*z;
return r;
}
}
- GNUPLOT出力結果
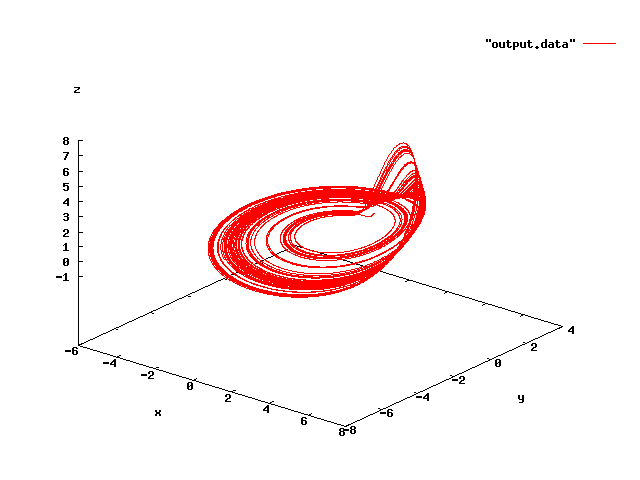
|
|
|
|
|
|