ここでは実際に離散的フーリエ変換を、簡単なのこぎり波に対して行ってみる。

• のこぎり波を生成するプログラム例

  #include <stdio.h>
  #include <math.h>
  
  #define max 100         //最大繰り返し回数
  
  int main()
  {
          int i,n,m;
          double x,y[max];
          
          n=0;
  
          FILE *function;
          function=fopen("function.data","w");
  
  //のこぎり波の一周期分の数値をつくる。
          for(x=-1.0;x<=1.0;x+=0.1) {
                  y[n]=x;
                  n++;
          }
  
  //のこぎり波の生成
          for(i=0;i<max;i++) {
                  for(m=0;m<n;m++) {
                          fprintf(function,"%f\n",y[m]);
                  }
          }
  
          fclose(function);
  
          return 0;
  }
  

  これを GNUPLOT で出力すると、

  

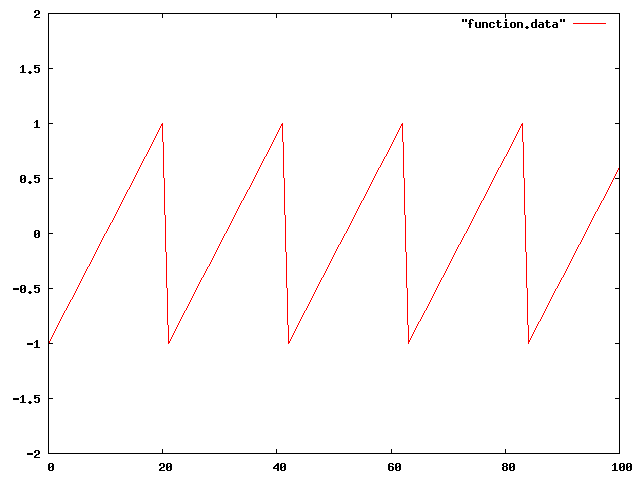
• フーリエ変換のプログラム例

  #include <stdio.h>
  #include <math.h>
  
  #define max 10000                       //Nの限界値
  #define pi 3.1415926535         //円周率
  
  int main()
  {
          int k,n,N;
          double f[max+1],ReF,ImF;
  
          FILE *function;
          FILE *fourier;
  //フーリエ変換したいデータをあらかじめファイル function.data に保存しておく
          function=fopen("function.data","r");
          fourier=fopen("fourier.data","w");
  
  //データの読み込み（ただし実数の成分のみ）
          for(N=0;N<max;N++) {
                  if(fscanf(function,"%lf",&f[N]) == EOF) {
                          N--;
                          break;
                  }
          }
  
  //実数部分と虚数部分に分けてフーリエ変換
          for(n=0;n<N;n++) {
                  ReF=ImF=0.0;
                  for(k=0;k<N;k++) {
                          ReF+=f[k]*cos(2*pi*k*n/N);
                          ImF+=-f[k]*sin(2*pi*k*n/N);
                  }
                  fprintf(fourier,"%d %f %f\n",n,ReF,ImF);
          }
  
          fclose(function);
          fclose(fourier);
          
          return 0;
  }
  

  GNUPLOTで出力結果を見てみる。上の画像が実数成分、下の画像が虚数成分である。

  横軸が周波数を表し、縦軸がその周波数の強さ（スペクトル）となる。

• 離散的逆フーリエ変換のプログラム例

  #include <stdio.h>
  #include <math.h>
  
  #define max 10000                       //Nの最大限度数
  #define pi 3.1415926535         //円周率
  
  int main()
  {
          int i,k,n,N;
          double Ref,Imf;
          double ReF[max+1],ImF[max+1];
          FILE *fourier;
          FILE *inversef;
  
  //逆フーリエ変換したいデータをあらかじめfourier.dataに保存しておく
          fourier=fopen("fourier.data","r");
          inversef=fopen("inversef.data","w");
  
  //データの読み込み。
          for(N=0;N<max;N++) {
                  if(fscanf(fourier,"%d %lf %lf",&i,&ReF[N],&ImF[N]) == EOF) {
                          N--;
                          break;
                  }
          }
  
  //フーリエ逆変換
          for(k=0;k<N;k++) {
                  Ref=Imf=0.0;
                  for(n=0;n<N;n++) {
                          Ref+=(ReF[n]*cos(2*pi*k*n/N)-ImF[n]*sin(2*pi*k*n/N))/N;
                          Imf+=(ReF[n]*sin(2*pi*k*n/N)+ReF[n]*sin(2*pi*k*n/N))/N;
                  }
                  fprintf(inversef,"%d %f %f\n",k,Ref,Imf);
          }
  
          fclose(fourier);
          fclose(inversef);
  
          return 0;
  }
  

  GNUPLOTで出力してみる。理論的には元ののこぎり波に戻るはずである。

  

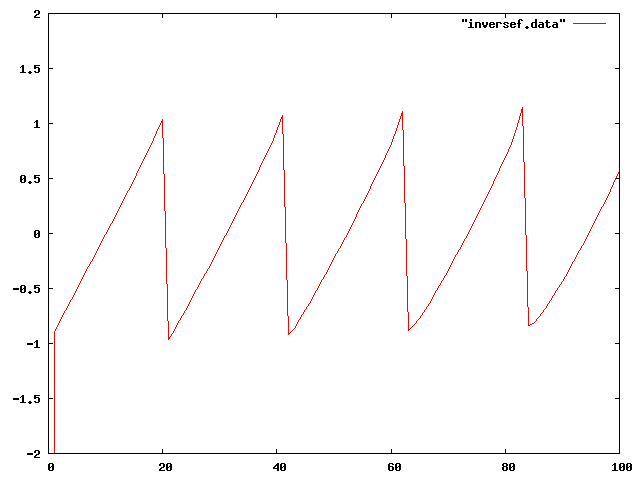
  やや違うところがあるがほぼ元ののこぎり波に戻った。しかし、もっと周波数が大きい部分では大きなずれが見られる。これは近似を行ったから誤差の発生はまぬがれないせいもあるが、比較的近似を粗く行ったせいもある。